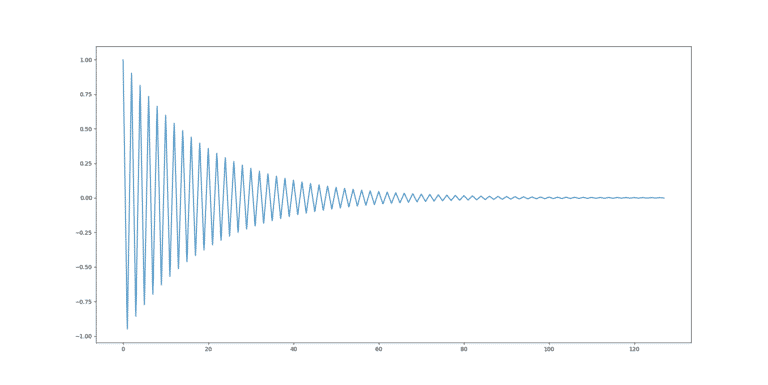
La descente du gradient
Introduction
Avant de rentrer dans le vif du sujet, il est important de préciser que la descente du gradient est très utilisée aujourd’hui. Notamment dans le domaine de l’apprentissage automatique. Par exemple, la grande majorité des intelligences artificielles (IA) à base de réseau de neurones artificiel, ont dû avoir recourt à l’utilisation de cette méthode pour “programmer” les neurones de l’IA.
Nous allons voir comment implémenter cet algorithme simplement.
Mise en situation
Il arrive que l’on soit fasse à un problème ne pouvant pas être résolu de manière directe. Par exemple, supposons que vous devez résoudre un problème d’ordre calculatoire, comme :
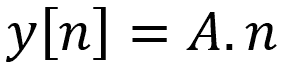
Eq.1 Fonction simple
Si votre objectif est de trouver ‘A’ (supposons que c’est la seule inconnue). Dans ce cas, la méthode directe vous permet décrire ‘A = y[n]/n’.
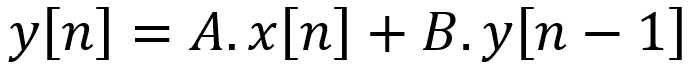
Eq.2 Fonction récursive
Pour les équations récursives comme celles ci-dessus, trouver directement ‘A’ et ‘B’ peut être (très) complexe et demander des compétences avancées en mathématique. Imaginez devoir résoudre plusieurs dizaines à plusieurs milliards de paramètres (comme ‘A’ ou ‘B’) pour une équation comme celle présentée ci-dessus, cette tache serait au moins très difficile voir impossible avec une méthode directe.
Dans certains cas, la méthode directe est un chemin long et douloureux, mais rien ne vous oblige à résoudre ce genre de problème via cette méthode. Car nous allons voir ici une autre approche bien moins complexe et demandant peut de connaissance pour être mis en place.
Explication de l’algorithme
Avant de passer au cas pratique, il est important de comprendre comment fonctionne cet algorithme.
L’algorithme de la descente du gradient vous permet de trouver un minimum dans une fonction (dérivable). Par exemple :
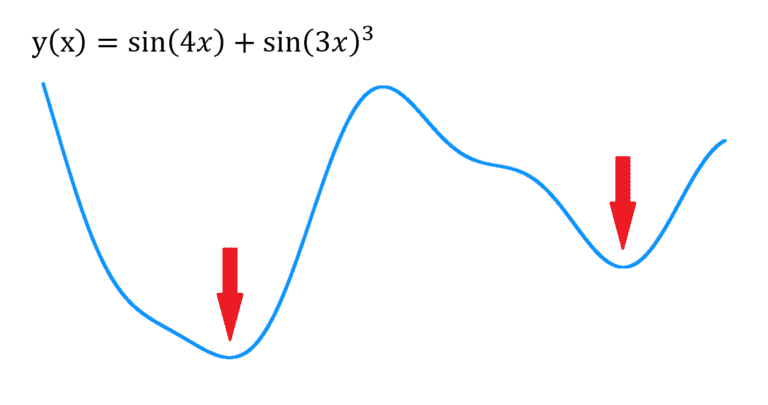
Fig.1 : Fonction 1D exemple
Dans la figure ci-dessus, on trouve deux minimums (sous les flèches rouges).
Avant d’aller plus dans le détail, je vais illustrer ce que fait une dérivée. Cette notion est importante pour comprendre la descente du gradient. Je parle bien de la notion, pas besoin de savoir dériver une fonction pour faire une descente du gradient. Je vais vous montrer dans les sections suivantes deux méthodes pour exécuter une descente du gradient :
- Une méthode passant par le calcul préalable des dérivées partielles.
- Une méthode par approximation des dérivées partielles (pas besoin de calculer les dérivées partielles).
Pour expliquer ce que fait une dérivée, je vais m’appuyer sur une illustration qui le montre graphiquement :
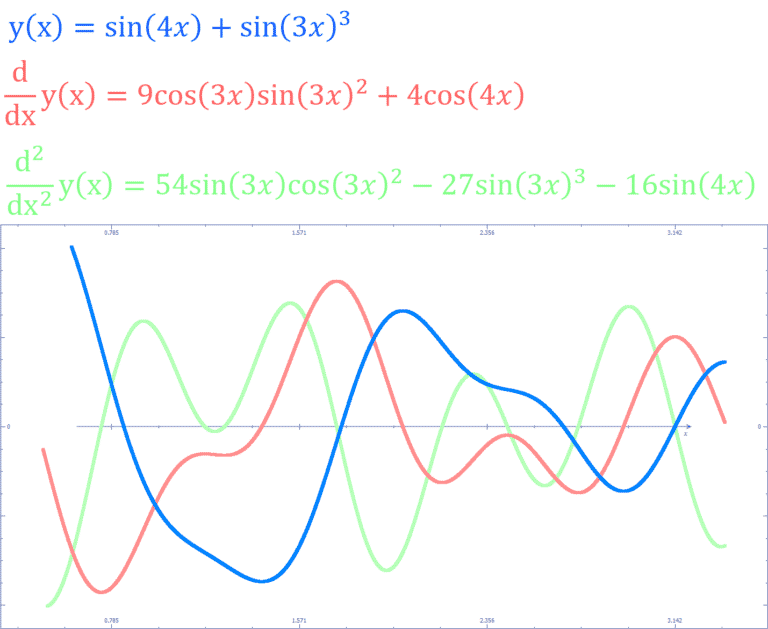
Fig.2 Fonction y; y’ et y”
La courbe bleu est la fonction originale qui dépend de ‘x’.
Par exemple sur la Fig.2 la courbe rouge est la dérivée de la courbe bleu. Vous remarquerez que lorsque la courbe bleu descend (en suivant l’axe ‘x’) la courbe rouge a des valeurs négatives et inversement lorsque que la courbe bleu monte la courbe rouge a des valeurs positives. Cela donne une information sur la direction dans laquelle évolue la courbe bleu en un point donné.
Vous remarquerez aussi que plus la valeur (axe ‘y’) de la courbe rouge s’éloigne de zéro, plus la courbe bleu accélère dans sa direction actuelle.
Pour finir, lorsque la courbe rouge prend la valeur zéros, cela veut dire que la courbe bleu n’évolue pas (elle ne monte pas / elle ne descend pas).
Il est donc possible avec un algorithme itératif (qui s’exécute étape par étape) de trouver un minimum en utilisant cette notion.
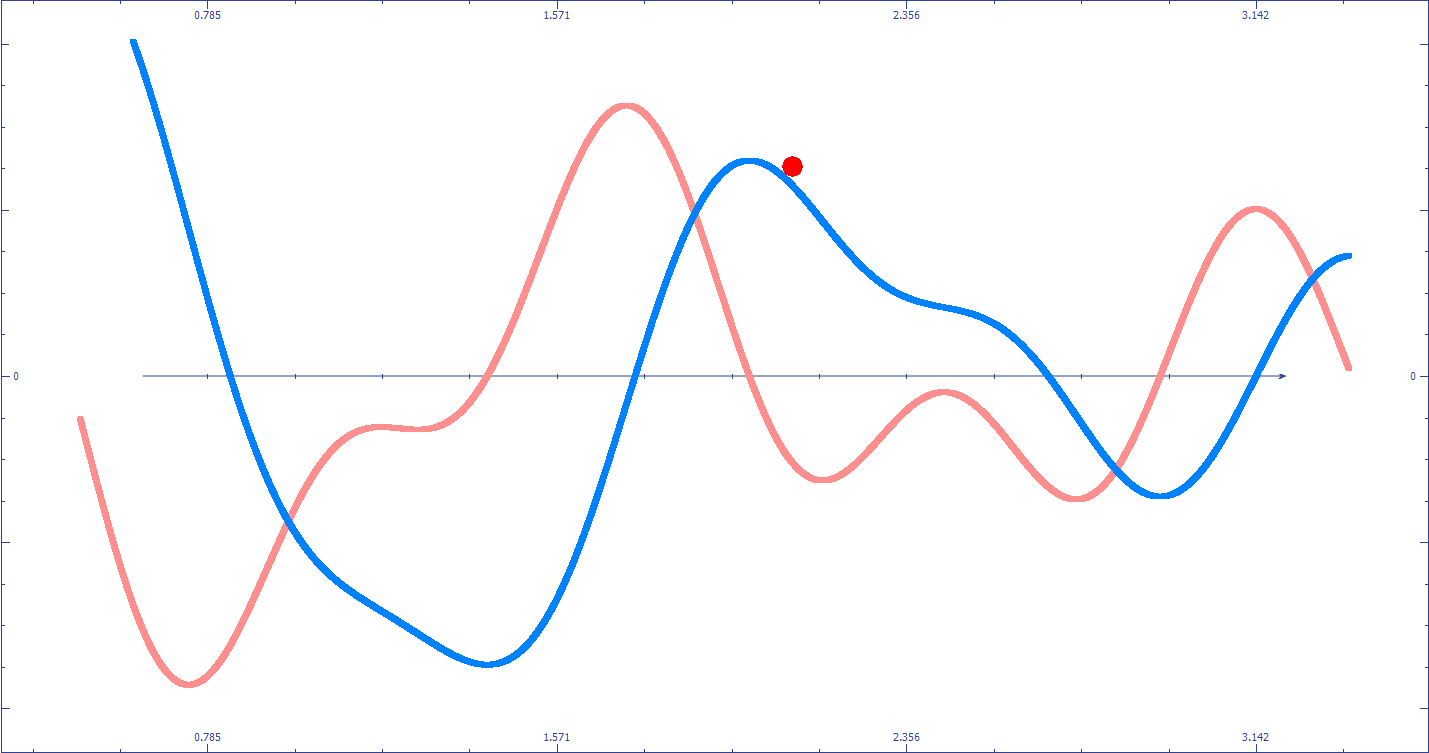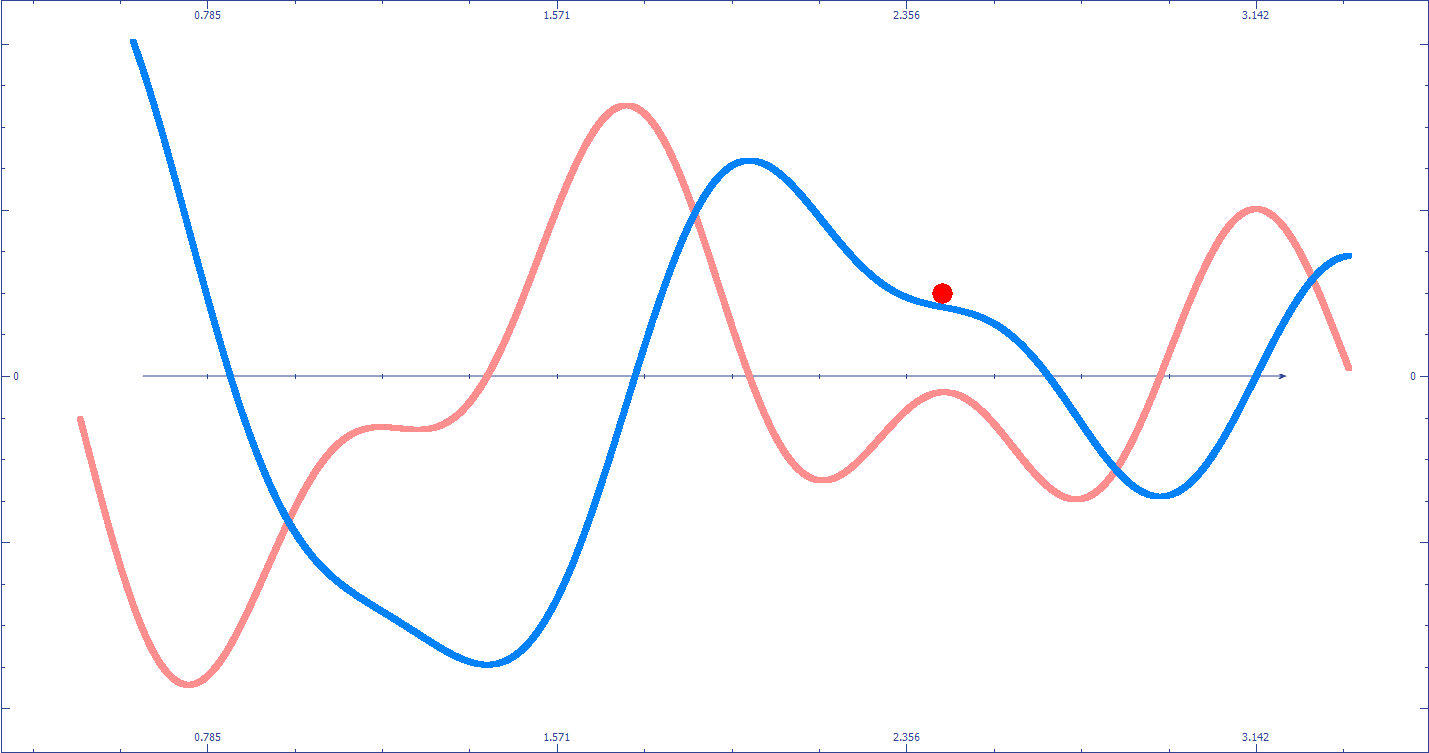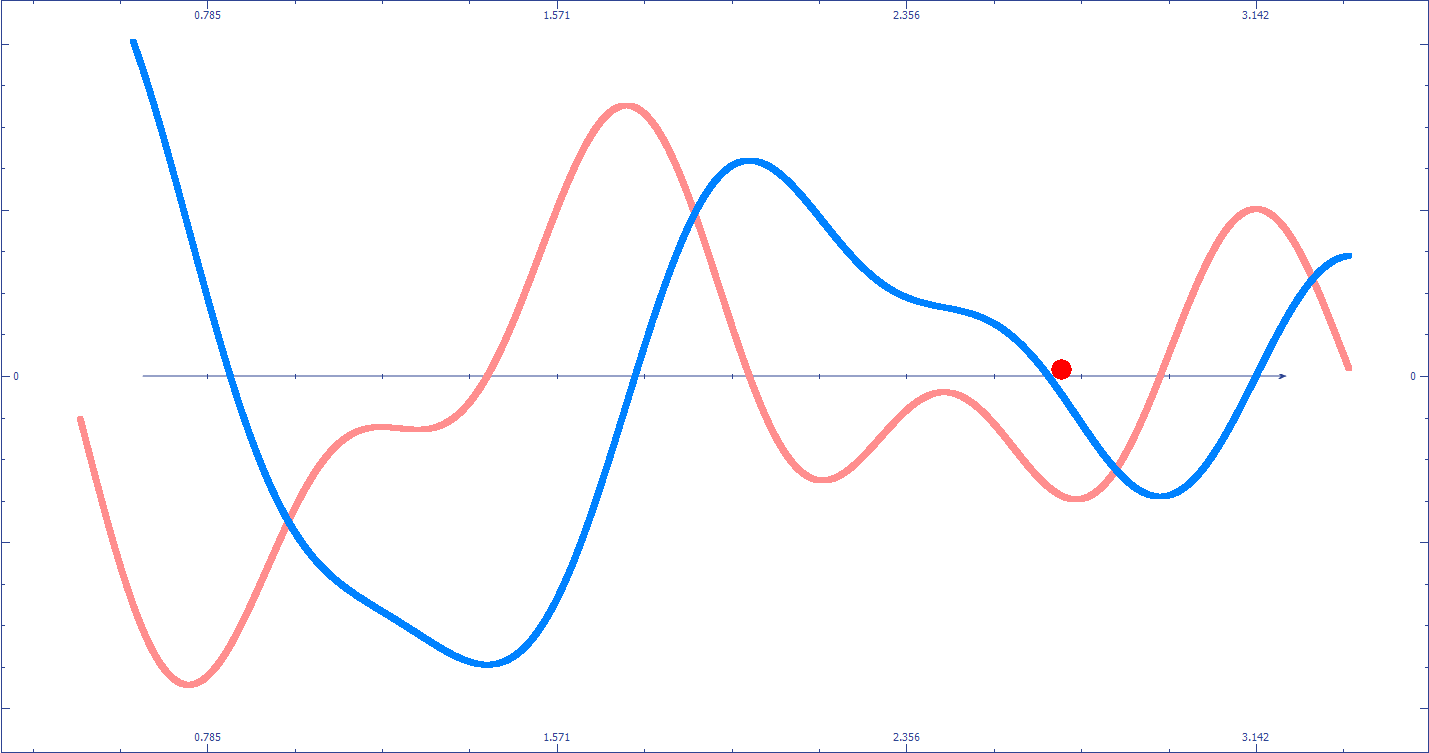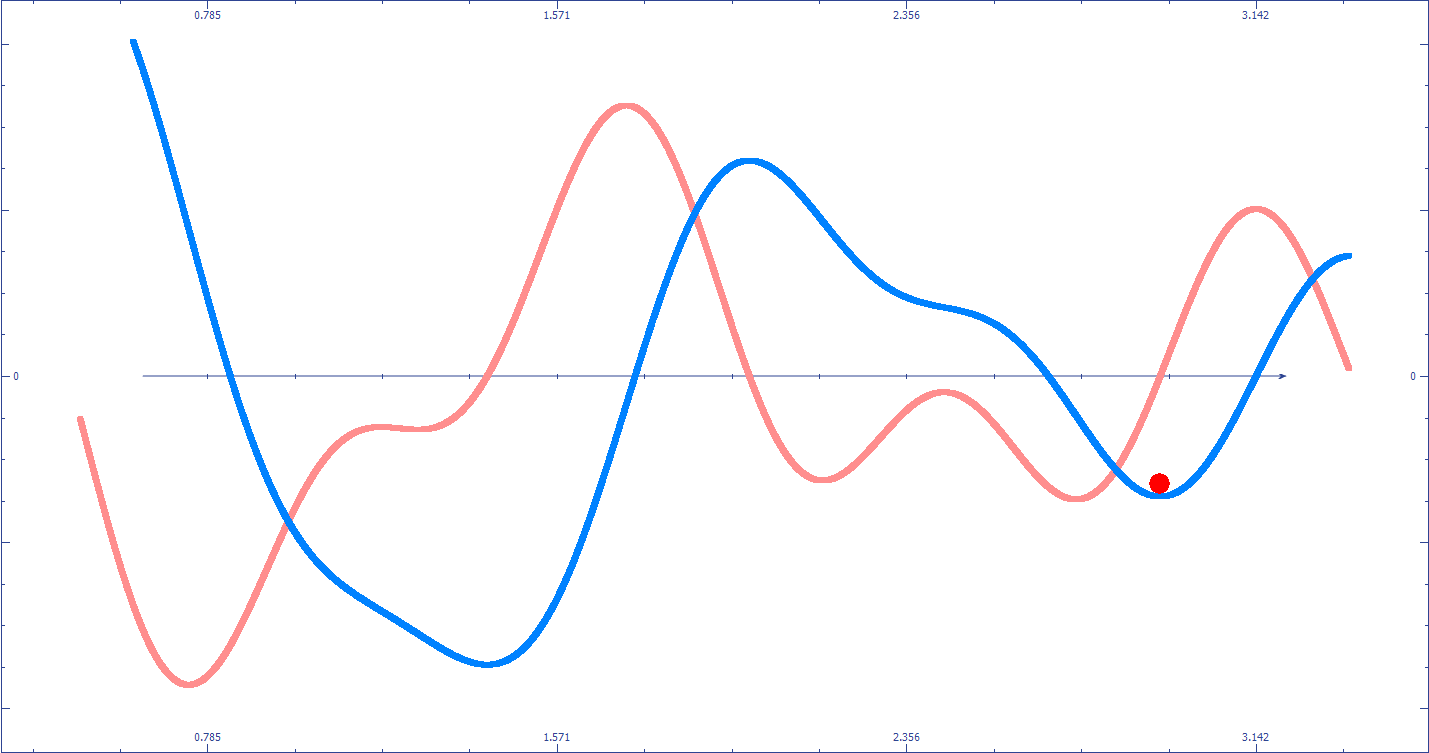
Fig.3 Illustration de la descente du gradient
L’animation Fig.3 rend compte de ce processus itératif, le point rouge (placé aléatoirement sur la courbe bleu) se déplace vers la droite lorsque le signe de la courbe rouge (la dérivée) est négative. Plus la valeur de la dérivée s’éloigne de zéros plus le point rouge avance rapidement. Lorsque la dérivée vaut zéros, le point ne bouge plus, un minimum a donc été trouvé.
Ce processus itératif porte le nom de descente du gradient.
La prochaine section met en avant l’utilité de savoir trouver des minimums.
La fonction objectif
On a vu comment trouver un minimum sur un signal, mais je n’ai pas précisé à quoi cela peut-il servir.
L’utilisation de la descente du gradient prend sens lorsque qu’elle est utilisée conjointement avec une fonction objectif (“loss function” en anglais).
Pour faire simple une fonction objectif met un score sur les données soumissent en paramètres. Un peut comme si vous devriez évaluer vos compétences en passant un examen, vous aller cherchez à avoir la note maximal, mais c’est l’examinateur qui va fixer la note.
Pour une fonction loss c’est a peut près de la même chose, elle prend généralement deux paramètres. Dans l’analogie faite plus haut, disons que votre compte-rendu de l’examen est l’un des paramètres et le second paramètre est la copie qu’il aurait fallu faire pour avoir la note parfaite (elle est estimée par l’examinateur).
Cependant une fonction loss vous donne zéros si vous faite le score parfait et un score supérieur a zéro si vous vous écartez de la perfection.
Formellement, cette comparaison se traduit par une simple soustraction.
On comprend désormais que l’utilisation de la descente du gradient pour trouver un minimum dans une fonction loss prend tout son sens. Cela permet de résoudre des problèmes au sens large (que ce soit directement ou via un model complexe comme un réseau de neurones).
Pour des taches de régressions l’une des fonction loss la plus utilisée est sans doute “Mean Squared Error” (MSE) ou l’erreur quadratique moyenne.
Eq.3 : MSE loss
‘Yi’ correspond aux données de référence et ‘Ýi’ correspond aux données a notées, ‘n’ correspond au nombre de données a notées.
Ce qu’il faut voir, c’est que la “magie” opère grâce à l’utilisation de la soustraction. Cette dernière permet de comparer les données prédites avec les données considérées vraies.
Maintenant que toutes les notions sont en place, on va pouvoir commencer l’implémentation d’une descente du gradient.
Implémentation – problématique
Pour l’implémentation, un exemple simple sera choisi.
Prenons l’équation présentée plus haut :
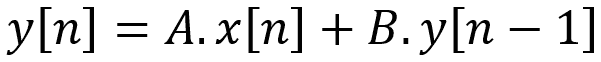
Eq.2 Fonction récursive
En réalité, cette équation a une fonction utile, elle permet d’élaborer des filtres numériques efficients. Résoudre ce genre d’équations peut avoir un intérêt, c’est ce que l’on va faire via la descente du gradient de deux façons :
- Sans calcul des dérivées partielles, elles seront estimées.
- Avec calcul des dérivées partielles.
Le but du jeu sera de faire correspondre ‘y[n]’ avec une cible connaissant ‘x[n]’. Pour y parvenir, il faut trouver les bonnes valeurs de ‘A’ et ‘B’. C’est ce que l’on va faire via la descente du gradient.
La fonction récursive étant infinie, on va arbitrairement fixer la longueur de la séquence à 128.
La fonction x[n] est définie comme suis :
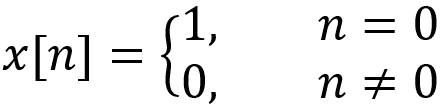
Eq.4 : Définition de x[n]
Ce qui se traduit graphiquement :
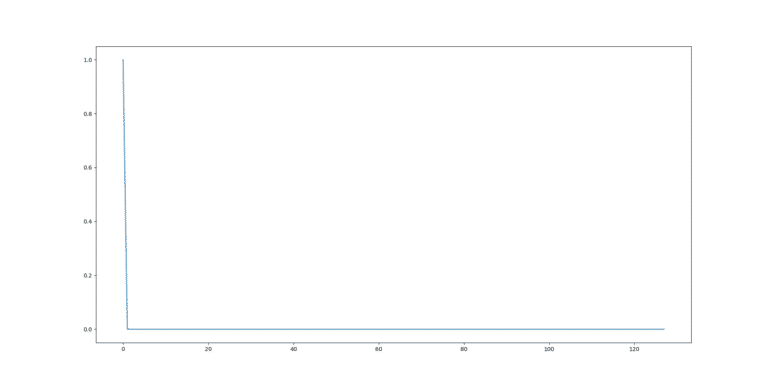
Fig.4 : Représentation graphique de x[n]
La fonction y[n] est définie comme suis :
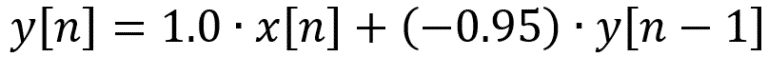
Eq.5 : Définition de y[n]
Ce qui se traduit graphiquement :
Fig.5 : Représentation graphique de y[n]
Pour y[n] j’ai réutilisé l’équation Eq.2 avec des valeurs arbitraires pour ‘A’ (1.0) et B (-0.95). Rien ne m’oblige à faire cela, y[n] aurait pu être n’importe quelle fonction (Il en va de même pour x[n]).
Réutiliser l’Eq.2 est un moyen de m’assurer que l’optimisation de A et B donnera de bon résultats avec la descente du gradient ce qui n’aurait pas été le cas si y[n] aurait pris les valeurs de l’équation de la Fig.1 car aucune valeur de ‘A’ et ‘B’ ne peut donner l’équation de la Fig.1 (avec x[n] = Eq.4).
Implémentation – sans calcul des dérivées partielles
Nous allons utiliser python 3 pour réaliser cette implémentation.
Pour la visualisation de la progression, la librairie ‘matplotlib’ est nécessaire. Elle peut être installée via la commande suivante:
pip install matplotlib
Initialisons le programme python :
import matplotlib.pyplot as plt
LEN = 128
EPOCH = 200
LEARNING_RATE = 1.0
LEARNING_RATE_DECAY_STEP = 50
LEARNING_RATE_DECAY_FACTOR = 4.0
EPSILON = 0.00001
‘LEN’ correspond à la longueur de x[n] et y[n], 128 est une longueur arbitraire.
‘EPOCH’ correspond au nombre d’étapes d’entraînement.
‘LEARNING_RATE’ est une constante utiliser pour ajuster le montant du gradient à mettre a jour. J’en reparlerai lorsque qu’il sera utilisé pour plus de clarté.
‘LEARNING_RATE_DECAY_STEP’ et ‘LEARNING_RATE_DECAY_FACTOR’ sont facultatifs. Je vais les justifier plus tard.
‘EPSILON’ est une constante permettant d’estimer les dérivées partielles.
On va écrire le code qui produit ‘y[n]’ en fonction de ‘A’ et ‘B’:
def reponseImpulsion(A, B):
#Definition des x[n] eq.4, plus zeros padding de 1 sur la gauche
impulsion = [0.0] * (LEN+1)
impulsion[1] = 1.0
#Execution de l'eq.2 (padding pour y[n] aussi)
y = [0.0] * (LEN+1)
for i in range(1, LEN+1):
y[i] = (A * impulsion[i]) + (B * y[i-1])
#Suppression du padding, y[n] a bien la longueur 'LEN'.
return y[1:]
#Definition des y[n] cibles (A=1.0 et B=-0.95)
CIBLE = reponseImpulsion(1.0, -0.95)
La fonction “reponseImpulsion” génère ‘y[n]’ à partir de la définition de ‘x[n]’ et des paramètres ‘A’ et ‘B’ fournis.
Cette fonction est utilisée pour générer la constante ‘CIBLE’. Il s’agit du ‘y[n]’ cible qui sera utilisée dans la fonction objectif. ‘CIBLE’ correspond a fig.5.
def lossMSE(y_true, y_pred):
mse = 0
for i in range(LEN):
mse += (y_true[i] - y_pred[i])**2
mse /= LEN
return mse
La fonction “lossMSE” exécute l’eq.3. Le paramètre ‘y_true’ correspond aux données de références tandis que le paramètre ‘y_pred’ correspond aux données calculées.
def gradient(A, B):
gradientA = 0.0
gradientB = 0.0
#Calcul l'erreur actuelle provoquée par les paramètres A et B
lossRef = lossMSE(CIBLE, reponseImpulsion(A, B))
#Esimation de la dérivée de A
A += EPSILON
loss = lossMSE(CIBLE, reponseImpulsion(A, B))
gradientA = (loss - lossRef) / EPSILON
A -= EPSILON#Remet A dans son etat initial
#Esimation de la dérivée de B
B += EPSILON
loss = lossMSE(CIBLE, reponseImpulsion(A, B))
gradientB = (loss - lossRef) / EPSILON
B -= EPSILON#Remet B dans son etat initial
return gradientA, gradientB
Cette fonction calcul les valeurs des dérivées partielles de ‘A’ et ‘B’ de la fonction objectif. Habituellement, ces valeurs sont nommées “gradients”. C’est ‘gradientA’ et ‘gradientB’ qui contient l’information de la direction et la force avec laquelle il faut modifier les paramètres ‘A’ et ‘B’.
Ici, les dérivées sont estimées avec une différenciation numérique. Cela est effectué par le bout de code suivant :
(loss – lossRef) / EPSILON
En effet, la définition formelle de la dérivée s’exprime comme suis :
Eq.6 : Définition de la dérivée
Ou,
‘f'(x0)’ : Correspond au gradient (la dérivée).
‘f(x0)’ : Correspond a la fonction objectif.
‘x0’ : Correspond a un des paramètres.
‘h’ : Correspond a un intervalle le plus proche possible de zéro (ici ‘EPSILON’).
Dit autrement, on fait varier d’une toute petite quantité un des paramètre (‘A’ ou ‘B’) pour voir comment le résultat de la fonction objectif varie. Cette variation nous donne le sens et la force avec laquelle on doit changer le dit paramètre pour atteindre un minimum.
Les framework de machine learning tel que Tensoflow et PyTorch utilisent une autres méthode similaire appeler différenciation automatique.
def main():
global LEARNING_RATE
#Définition des parametres a optimisées
A = 0
B = 0
#Prépare l'affichage du résultat
true, = plt.plot(CIBLE)
line, = plt.plot(CIBLE)
plt.legend((true, line), ('CIBLE', 'Prédiction'))
for e in range(EPOCH):
#Optimise les parametres A et B en fonction des gradients
gradA, gradB = gradient(A, B)
A -= gradA * LEARNING_RATE
B -= gradB * LEARNING_RATE
#Regle d'apprentissage facultative
if (e+1) % LEARNING_RATE_DECAY_STEP == 0:
LEARNING_RATE /= LEARNING_RATE_DECAY_FACTOR
#Calcul pour le graph seulement
pred = reponseImpulsion(A, B)
loss = lossMSE(CIBLE, pred)
print("{0:4d} / {1:4d} : loss {2: .6f}".format(e+1, EPOCH, loss))
#Affichage du graph
line.set_ydata(pred)
plt.title('A={} B={}'.format(A, B))
plt.draw()
plt.pause(0.001)
La correction/optimisation des paramètres s’effectue dans la boucle d’entraînement.
On met à jour les paramètres avec leurs gradients respectifs. Il faut soustraire le gradient pour toujours avancer vers un minimum. (voir fig.3 pour vous en convaincre).
La variable ‘LEARNING_RATE’ permet d’ajuster la force avec laquelle on veut mettre à jour les paramètres. Généralement, cette valeur est inférieure à 1.0.
La règle d’apprentissage permet de gérer la vitesse d’apprentissage au fil de l’entraînement. Cette fonctionnalité est totalement facultative.
Exécuter la fonction ‘main’ donne le résultat suivant :
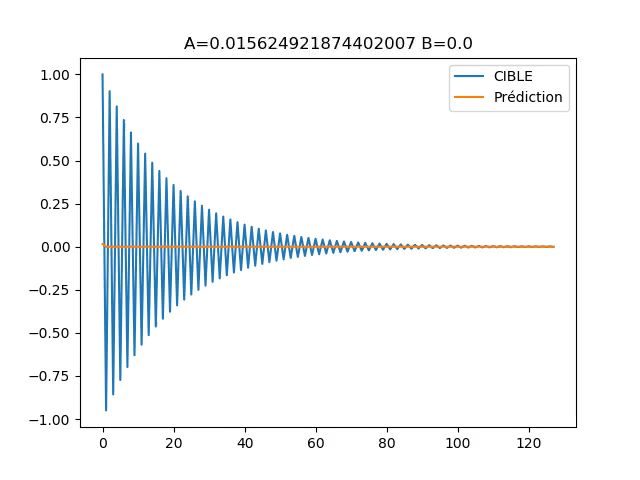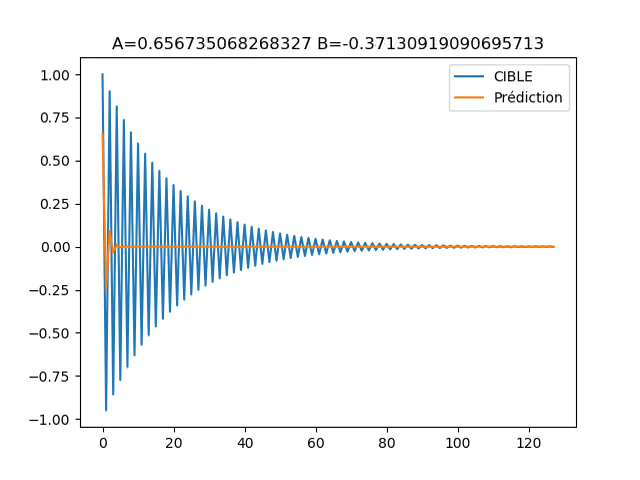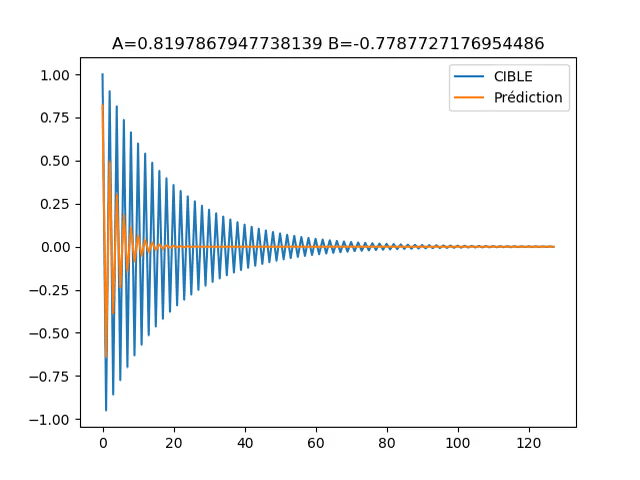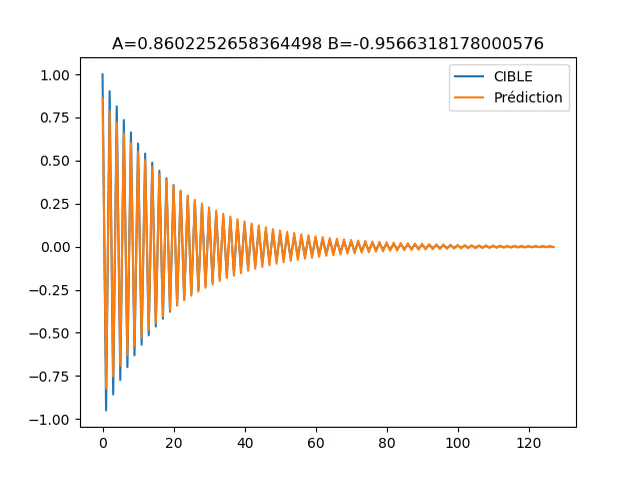
Fig.6 : Visualisation de y[n] prédit versus y[n] cible
On peut voir que la descente du gradient fonctionne comme espérée. Si l’aspect design de filtre numérique vous intéresse notre application téléphone (gratuite) “IE-Concept Toolbox” vous permet d’utiliser la descente du gradient pour désigner un filtre à partir de sa réponse fréquentielle.
Implémentation – à partir du calcul des dérivées partielles
La majorité du code reste quasiment inchangé, excepté la fonction ‘gradient’.
Avant de changer la fonction gradient, il faut définir les dérivées partielles en fonction du paramètre ‘A’ et ‘B’.
La fonction objectif (Eq.3) se dérive en fonction du paramètre ‘A’ de cette façon :
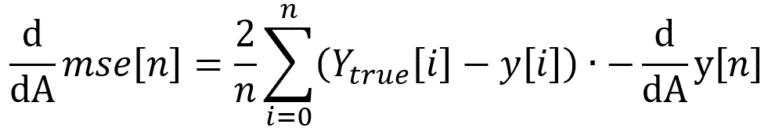
Eq.7 : Dérivée partielle en ‘A’ du loss MSE
Ou la dérivée partielle de y[n] (Eq.2) de ‘A’ s’écrit :
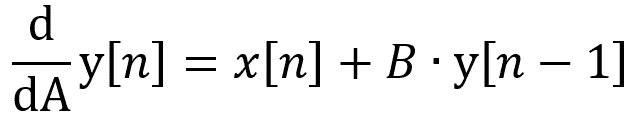
Eq.8 : Dérivée partielle de ‘A’, de l’équation récursive
De la même manière, il faut écrire les dérivées partielles pour ‘B’:
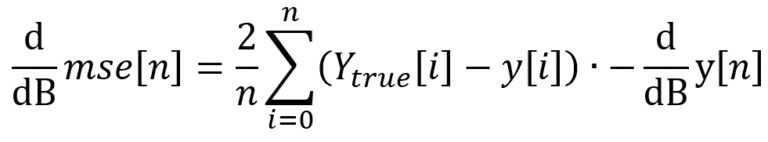
Eq.10 : Dérivée partielle de ‘B’ du loss MSE
Ou la dérivée partielle de y[n] (Eq.2) de ‘B’ s’écrit :
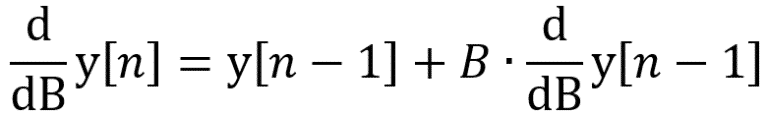
Eq.11 : Dérivée partielle de ‘B’ de l’équation récursive
Code du calcul de la dérivée partielle de ‘A’ :.
def dpA(A, B):
impulsion = [0.0] * (LEN+1)
impulsion[1] = 1.0
#Calcul de Eq.8
y = [0.0] * (LEN+1)
dy = [0.0] * (LEN+1)
for i in range(1, LEN+1):
y[i] = (A * impulsion[i]) + (B * y[i-1])
dy[i] = impulsion[i] + (B * y[i-1])
y = y[1:]
dy = dy[1:]
#Calcul de Eq.7
y_true = CIBLE
mse = 0
for i in range(LEN):
mse += (y_true[i] - y[i]) * -dy[i]
mse *= 2
mse /= LEN
return mse
Code du calcul de la dérivée partielle de B :
def dpB(A, B):
impulsion = [0.0] * (LEN+1)
impulsion[1] = 1.0
#Calcul de Eq.11
y = [0.0] * (LEN+1)
dy = [0.0] * (LEN+1)
for i in range(1, LEN+1):
y[i] = (A * impulsion[i]) + (B * y[i-1])
dy[i] = y[i-1] + (B * dy[i-1])
y = y[1:]
dy = dy[1:]
#Calcul de Eq.10
y_true = CIBLE
mse = 0
for i in range(LEN):
mse += (y_true[i] - y[i]) * -dy[i]
mse *= 2
mse /= LEN
return mse
Voici le code de la fonction qui calcul le gradient :
def gradient(A, B):
gradientA = 0.0
gradientB = 0.0
#Calcul l'erreur actuelle provoquée par les paramètres A et B
lossRef = lossMSE(CIBLE, reponseImpulsion(A, B))
#Calcul de la dérivée partielle de A
gradientA = dpA(A, B)
#Calcul de la dérivée partielle de B
gradientB = dpB(A, B)
return gradientA, gradientB
Après exécution, il est nécessaire de changer ‘LEARNING_RATE_DECAY_FACTOR = 4’ à 3.75.
Cette différence est causée par la nature moins précise des valeurs des dérivées estimées dans la section précédente.
Avantages/Limites de la descente du gradient
La plupart des exemples montrés sont simples est peuvent être résolues via une méthode directe.
Cependant, lorsque vous augmentez le nombre de paramètres, cela peut ne plus être le cas et la méthode itérative (comme la descente du gradient) peut être une nécessitée.
À titre d’exemple, la plupart des réseaux de neurones profonds possèdent ~100 millions de paramètres, cela peut atteindre 175 milliards de paramètres dans les cas extrêmes, la descente du gradient fonctionne toujours dans ces conditions.
De plus, la descente du gradient va vers le résultat ou une autre méthode itérative comme les algorithmes génétique (GA) cherche un peu au hasard. La pratique montre qu’il est bien plus difficile (pour ne pas dire impossible) d’entraîner un réseau de neurones avec un GA.
Cependant, il y a des limites connues :
La descente du gradient peut être “piégée” dans un minimum local qui ne correspond pas au minimum global (le meilleur résultat possible). Cela dépend entre autres du point de départ de vos paramètres.
Votre model peut faire exploser/disparaitre le gradient, c’est à dire que la valeur du gradient devient soit trop petite soit trop grande pour être stockée sur une machine. Cela ruine l’apprentissage (essayez de mettre la constante ‘LEARNING_RATE’ à 2.0).
Il faut ajuster des hyper-paramètres (learning rate, nombre d’epoch, règles d’apprentissage, etc) pour obtenir une bonne optimisation.
L’exemple implémenté rend compte de cela, car il possède une grande zone (en ‘A’=0 et ‘B’=0) ou le gradient est faible, ce qui encourage un fort learning rate. En même temps, le gradient tend exponentiellement vers l’infini a l’approche de ‘B’=-1. Ce qui rend dangereux un learning rate trop fort.
Le bon compromis entre nombres d’epoch / stabilitée est effectué par une règle d’apprentissage avec un learning rate décroissant au cours du temps.
L’ensemble de votre model (fonction loss compris) doit être dérivable pour chacun des paramètres. Cependant en machine learning il est courant d’avoir un model qui n’est pas 100% dérivable (activation ReLU, loss MAE, etc.). Dans ce cas il faut définir une valeur aux points non-dérivables. De même pour les opérateurs non-différentiables, par exemple l’opérateur ‘argmax’ peut être remplacé par son équivalent soft comme l’opérateur ‘softmax’ qui lui est dérivable.
Bien sûr, il existe plusieurs astuces pour limiter/contourner les défauts (model avec fonction d’activation spécifique, normalisation, fonction loss appropriée, utiliser un algorithme d’optimisation plus élaboré comme Adam, etc).